
-
Courses
- Courses
- GREEN BELT WITH LEAN FOCUS
- LEAN SIX SIGMA GREEN BELT
- OPTIMIZE VISION SYSTEMS
- METHODS FOR EFFECTIVE LEADERSHIP
- Practical Data Analysis
- Coaching For Lean Six Sigma
- Improving Indirect Processes
- World class Business Processes
- Lean Implementation Expert
- Lean metrics
- Must Knows for effective Calibration
- Improve process capability
- Systematic problem solving
- Lean Six Sigma Champion
- Lean Champion
- Cost Reduction
- Scrap Reduction
- Basic Statistics
- DMAIC
- Overall Equipment Effectiveness
- Lead time
- Process Mapping
- Process Stability
- Poka Yoke
- Systematic Problem Solving
- Value and Waste
- Custom courses
- Events
-
How to
- How to
- How to reduce scrap
- 5S
- 5 Why
- Attribute Agreement Analysis
- BOB WOW
- Creativity Techniques
- Critical to Quality (CTQ)
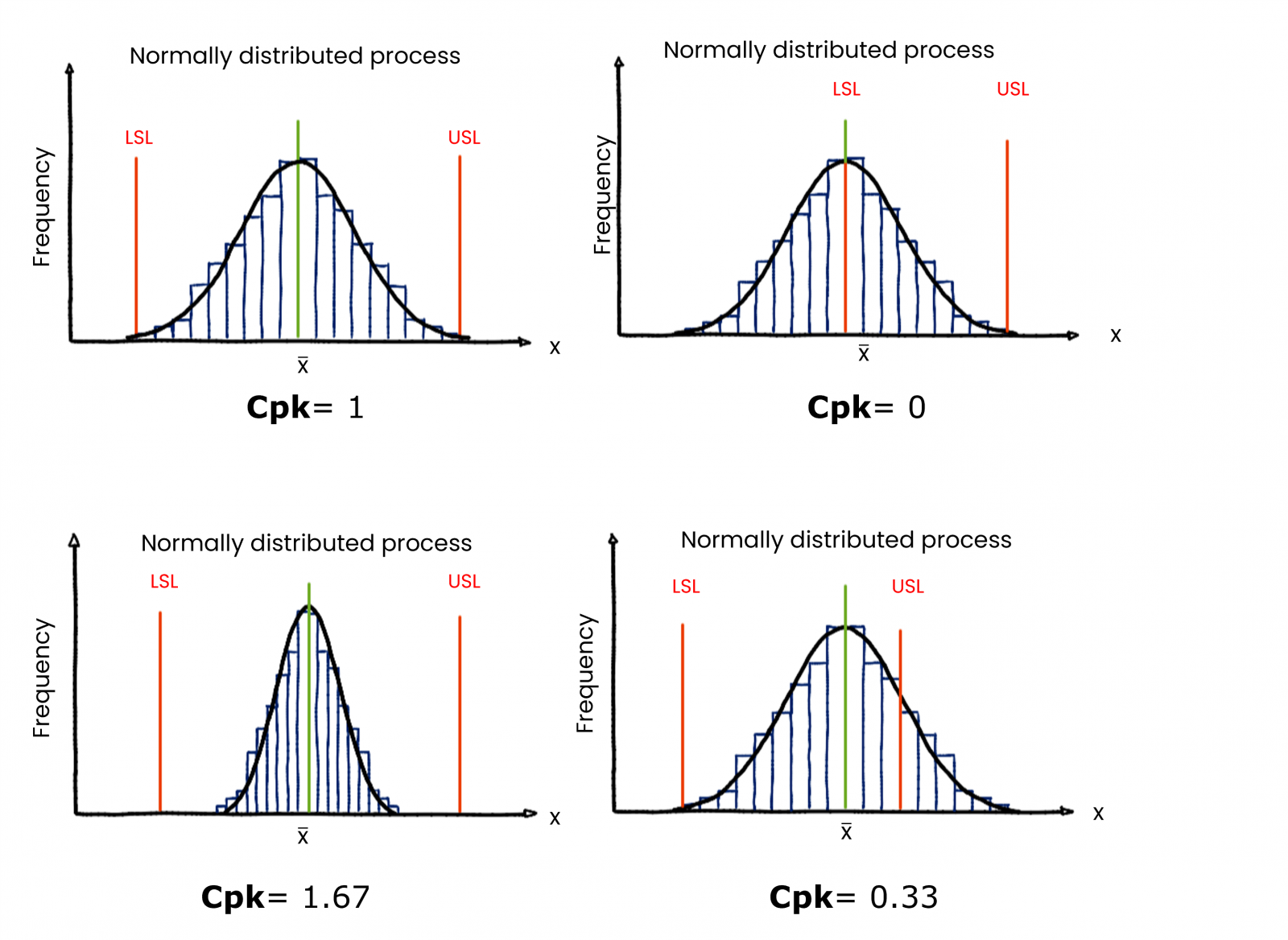
- Cpk
- Cpk vs Ppk
- Data Collection Plan
- Days of Inventory (DOI)
- Discrete Data
- DMAIC
- First Pass Yield (FPY)
- Gage R&R
- Gemba
- Ishikawa
- Lead Time
- On Time, In Full (OTIF)
- OEE
- Ppk
- Process Mapping
- Productivity
- Pull
- Scheduled Operating Time
- SIPOC
- Swimlane Diagram
- Takt Time
- Total Time
- Throughput Time
- Value Steam Mapping
- Work In Progress
- Contact us
- Log in



.png)
.png)

.png)
.png)


.png)
